How to Choose the Right Screening Design!

New DoE-users often get overwhelmed by the amount of different designs that are available. Instead of seeing the benefits of just using the DoE (Design of Experiments) approach at all the tend to worry how to choose the right design for a given application. In this piece I will present my approach to choose the right screening design while introducing a JMP-script that supports you with that.

When setting up a design to make some research about an unknown process we often start with so called screening designs. These are designs allowing you to analyze the effect of many factors with a relatively small number of experiments. Over the years I developed a small checklist that helps me keeping track of the important decision-points when setting up a screening design.

The very first subsection of my checklist are reconsiderations:

1. What is my overall goal?
2. What are my responses? How do I measure them?
3. What factors should be considered? In which ranges?
4. Are there block-factors?
5. Is it a split-plot problem?
6. Are there problematic combinations of factor settings?

Let's assume we are doing the paper helicopter experiment. 

1. Goal: Maximize the flight time.
2. Response: Flight time (s/10)
3. Of course the factors that are chosen vary from time to time. The factors in table 1 are the ones I used in a training in Berlin last week.
4. No block-factors.
5. No split-plots.
6. No problematic combinations of factor settings.

Table 1: Factors for the Paper Helicopter Experiment

All of those reconsiderations are very crucial to the success of a DoE - and none of them requires statistics knowledge. This is why I - as a statistician - want to focus on the next step: 

Design Choice

After we did all the hard work, the rest should be easy. We just need to figure out which design is the right one for our problem. Of course there are many different screening designs. Depending on which software you use you will see:

• Full-Factorial Designs
• Fractional-Factorials
• Definitive Screenings
• Plackett-Burman
• Orthogonal Arrays
• D-Optimal Designs
• Min-Run Resolution V, IV
• ...

To decide for one of those it is of course useful to understand the specific designs and nothing is better than knowing the strengths and weaknesses of each individual design. Non the less I want to provide a more general approach to chose a design even without knowing each individual design. Therefore I will compare all of these designs in terms of power, aliasing and size. In most DoE-software packages this involves setting up each individual design to do power-analysis and get an aliasing-report. To ease that step I created a script that will do most of the work for you in JMP (You will find the script here).

Using the JMP-Script

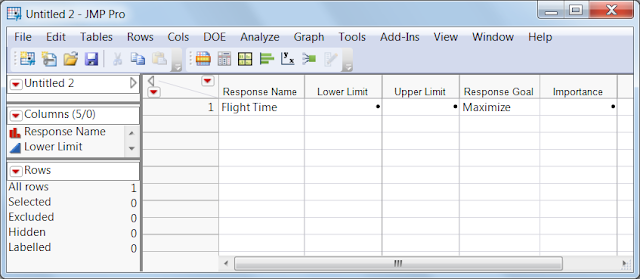
The script requires you to set up two data tables before we may start. The first table should contain all the information about your responses.

The second table has a different structure and cares for the factors of your problem.

Probably the easiest way to create these tables is to go to the Main Menu -> DOE -> Custom Designer

In there enter all responses and factors as you are used to it. Then use the hotspot at Custom Design (the red triangle) and Save Factors and Save Responses.

Now we are ready to go. Open the script, right click somewhere in the script and klick on Run Script.

Now we have to provide some additional information for the power analysis. 

• What is the desired level of significance?
• What is you anticipated coefficient (basically: relevant difference/2)?
• And what is your experimental error?

For the helicopter experiment a difference to detect of 0.5s (thus a coefficient of 0.25s) sounds reasonable for me. Having done this experiment probably 50 times already I have some amount of experience with the experimental error. It tends to be around 1/3rd of a second. Usually I plan a bit conservatively: 0.35s might be a good value. If you are not completely familiar with power analysis this and this might be a good starting points for you to read.

The last thing we have to do, is to tell JMP which data set contains the information about the responses and which one is about the factors. In my case Untitled 2 was for the response, Untitled was for the factors. The script isn't actually the fastest piece of code - apologies for that. After a while you should see this report:

The first section gives you the power for your different designs. All values below 0.8 are red, all other values are green. Usually we want screening experiments to achieve a power of at least 80%. For our example we see that the Definitive Screening and the Fractional Factorial Resolution 3 are out of contention. 

You might want to check if the aliasing of the Fractional Factorial Resolution 4 is ok for your purposes. Therefore open the corresponding outline item.

Colormap of Correlations - Fractional Factorial Resolution 4

As you can see there is quite some aliasing going on in this design. Personally I would not feel comfortable having some aliasing between 2-factor-interactions like Wing Length*Wing Width (=airofoil) or Wing Length*Weight. Thus the Fractional Factorial Design Resolution 4 does not seem to be an option, neither.

As the Full Factorial design, like the Fractional Factorial Design Resolution 5 have no issues with aliasing at all, I recommend using the Fractional Factorial Res. 5 in this case. It uses less runs but still has sufficient power.

To get the design just press the button Fractional Factorial (Res.5) at the bottom of the report and it will appear. 

Fractional Factorial Design Resolution 5

Time for some helicopter producing! Have fun!

P.S.: Currently the script only supports these five different designs. But it is easy to add other design. Just tell me about your preferred screening designs in JMP and I will add it whenever I have the time!